This submodule contains utility functions related to stitching of the compositional graphs to form graph complexes, so that much more complex graphs can be built from simpler ones while retaining homogeneous structure of the space. Furthermore, one can keep track of provenance of the subgraphs and use this information to deploy computational (e.g., ML) models on per-subgraph basis, which should be extremely useful for (a) combining the power of many specialized models and (b) creating stacked spaces for multi-step problems broken down into individual steps.
For typical use, please consult the findStitchingPoints function. As usual, if you compile stitching.nim as a Python library (.so file on Unix or .pyd on Windows), the findStitchingPoints_py will be available, taking the same arguments as findStitchingPoints in nim and returning a native Python dict.
Navigation: nimplex (core library) | docs/changelog | utils/plotting | utils/stitching
Procs
func compareNodes(a: int; b: int; nodeCoordinateTensor: Tensor[int]; priorityList: seq[int]): int {....raises: [], tags: [], forbids: [].}
- Comparator function to evaluate the order of two node numbers a and b based on their coordinates in the compositional space given in nodeCoordinateTensor of ints (e.g. simplex_grid output or the first element in the simplex_graph output tuple), ranked by the priorityList establishing order of dimensions in the ordered subspace one may be interested in. Source Edit
proc findStitchingPoints(dim: int; ndiv: int; maxDim: int = 3; components: seq[ string] = generateAlphabetSequence(dim); offset: int = 0): Table[string, seq[int]] {....raises: [KeyError], tags: [], forbids: [].}
-
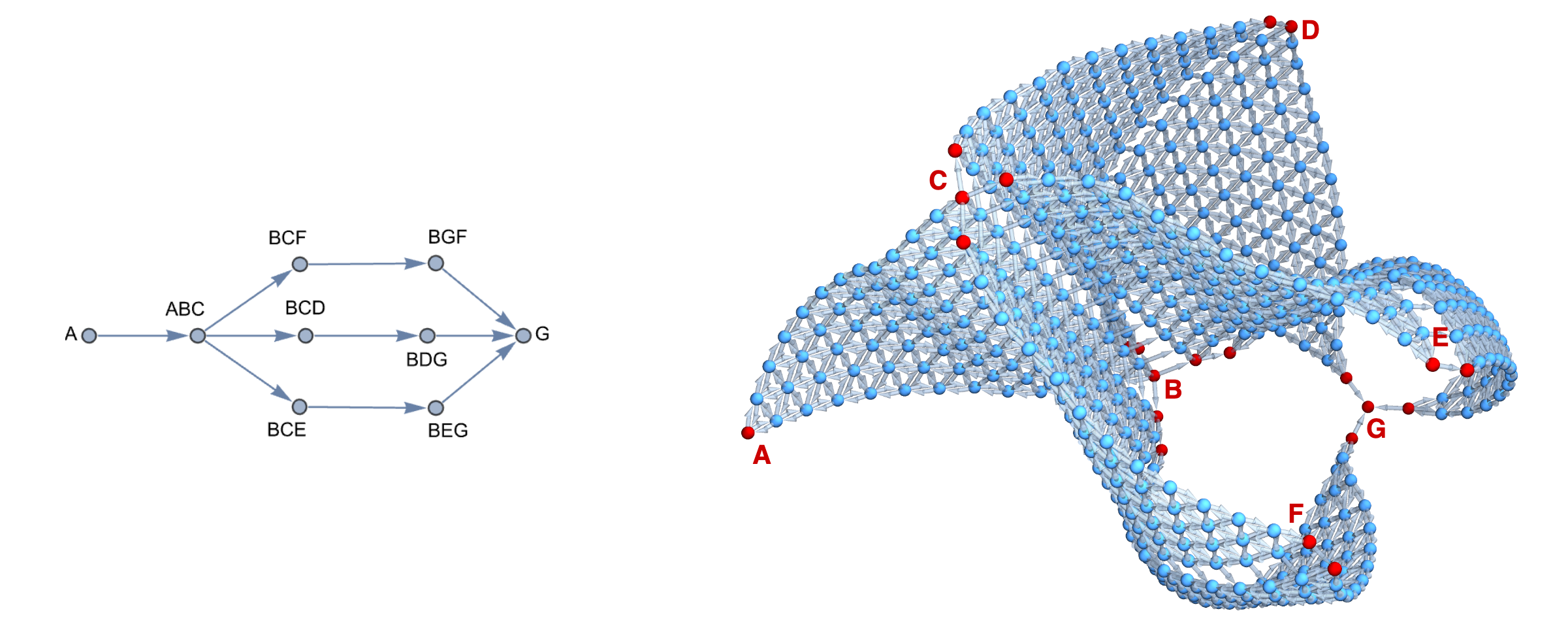
Main functionality of the module. It finds all ordered spaces and subspaces (up to the maxDim order) belonging to a simplex grid in dim-dimensional space with ndiv divisions per dimension, and identifies corresponding sequences of stitching points (simplex grid/graph nodes) for each of them, so that they can be used to join graphs together or otherwise establish equivalence between points in different spaces (where they overlap). The components parameter is optional and can be used to provide custom names for the space components (e.g., ["Ti64", "V", "SS316L"]). The output is a Nim Table (translated into Python dict if you use bindings) with keys being the names of the spaces/subspaces and values being the sequences of stitching points in the compositional grid.
You will typically run this function for each space you want to stitch, changing the dim to match dimensionality of the given space and components to match the order of components in the space. With the sets of points in hand, you can iterate over them creating edges to join the graphs together. As you can see in the example below, you don't need to order components in any specific way and can mix-and-match different dimensionality spaces as well.
Example:
import std/tables let stitch1Table = findStitchingPoints( 3, 12, components = @["TiAlloy", "CrV", "VNi"]) let stitch2Table = findStitchingPoints( 5, 12, components = @["AlCr", "VNi", "Hf90Zr10", "Ti5Zr95", "TiAlloy"]) echo "Subspace 1: ", stitch1Table["TiAlloy-VNi"] # Subspace 1: @[90, 88, 85, 81, 76, 70, 63, 55, 46, 36, 25, 13, 0] echo "Subspace 2: ", stitch2Table["TiAlloy-VNi"] # Subspace 2: @[0, 91, 169, 235, 290, 335, 371, 399, 420, 435, 445, 451, 454]
Source Edit func findSubspace[T](lst: seq[T]; maxDim: int = 3): seq[seq[T]]
- Finds all possible (unordered) subspaces of the input list lst up to the dimension maxDim. The list can be of any type and macro will handle it returning a list of lists of the same type. The default maxDim is set to 3 because for larger spaces, especially high dimensional ones, the number of subspaces grows rapidly (e.g. 1,956 for d=6) and computer memory can be exhausted quicker than anticipated when working on it in more intense steps; user can set it to any value they want though. Source Edit
func generateAlphabetSequence(length: int): seq[string] {....raises: [], tags: [], forbids: [].}
- Generates a sequence of strings of length length containing all UPPER and lower case letters of the alphabet. The primary purpose of this function is to generate unique names for space (A-B-C-D) and its ordered subspaces (e.g., A-B, B-A) if no custom names are provided by the user. Source Edit
func isSubspace(subSpace: seq[int]; space: seq[int]): bool {....raises: [], tags: [], forbids: [].}
- Small helper function to check if the input subSpace is a subspace of the space. Source Edit
func nonZeroComps(p: Tensor[int]): seq[int] {....raises: [], tags: [], forbids: [].}
- Finds the indices of non-zero components in the input tensor p to determine which (unordered) space/subspace it belongs to. Source Edit
func permutations[T](s: seq[T]): seq[seq[T]]
- Generates all possible permutations of the input sequence s using a recursive algorithm. Can accept any type of sequence thanks to Nim's powerful type system and reurns a sequence of sequences of the same type. Source Edit
func space2name(space: seq[int]; components: seq[string]): string {....raises: [], tags: [], forbids: [].}
- Converts the space/subspace represented by the indices in space to a string representation using the names of the components. It can be used in conjunction with generateAlphabetSequence too. Source Edit